A 6^th-order Tesla Magnifier

(or a transformer-coupled triple resonance network with distributed load capacitance)

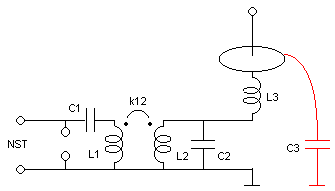
By April 2003 I started experiments with a 6th-order Tesla magnifier, in an attempt to verify if the design method developed for triple resonance networks can be also useful for an application intended for the production of sparks and streamers, a variation of the classical Tesla coil. The 6th-order Tesla magnifier consists in a low-impedance primary LC tank circuit L₁-C₁ magnetically coupled to a medium-impedance tank L₂-C₂, used as a "driver" for a high-impedance resonator formed by the third coil L₃ and its distributed load capacitance C₃. The device is powered by a neon sign transformer (NST) that has a spark gap across its output. The NST charges C₁ to the firing voltage of the gap, and while the gap conducts the circuit executes a transient involving symultaneous oscillations at three frequencies that, with proper design, ideally transfers all the energy initially stored in C₁ to the distributed capacitance C₃, producing pulses of very high voltage because C₃<<C₁. I had previously experimented with a directly coupled version of this circuit, that resulted in just reasonable performance. Directly coupled multiple resonance networks have the voltage gain associated with the number of oscillation cycles required for complete energy transfer, and so are quite inflexible. With the use of magnetic coupling, it's possible to remove this dependency, and so, in principle, to achieve better efficiency by reducing the energy transfer time.

My system was designed for operation in mode 3:4:5, what means that the energy transfer transient has oscillations at three frequencies that are in this ratio. I used the same C₁, L₃, and C₃ that I had prepared for previous experiments. With the help of the design formulas shown here, the remaining elements L₁, L₂, C₂, and the coupling coefficient k₁₂ can be calculated. The program mrn6 can make the calculations and plot the expected ideal waveforms. The result was:

C₁ = 5.08 nF
L₁ = 62.02 µH
C₂ = 79.64 pF
L₂ = 3.948 mH
C₃ = 9.8 pF
L₃ = 28.2 mH
k₁₂ = 0.3504
Voltage gain: 22.77
Energy transfer time: 6.606 µs

The driver transformer was designed with the help of the program Inca, that can calculate inductances and mutual inductances with great precision. L₁ was made as a flat coil and L₂ as a short solenoidal coil. This configuration produces the required quite high coupling, but doesn't present serious insulation problems.

Primary: 14 turns; internal radius = 8 cm; external radius = 12 cm; wire diameter = 1 mm (#18).
L₁= 0.06207 mH
Secondary: 176 turns; length = 10.2 cm; radius = 7.4 cm; wire diameter = 0.51 mm (#24); height above L₁ = 7.5 mm
L₂= 3.949 mH
Mutual Inductance M = 0.1734 mH
Coupling coefficient k₁₂ = 0.3501

The capacitance C₂ consists in the distributed capacitance present in the interconnection between L₂ and L₃ and in a lumped capacitor that completes it to the required value. The distributed capacitance can be estimated as somewhat larger than the sum of the Medhurst capacitances of L₂ (7.1 pF) and L₃ (5.6 pF), for the configuration used. To determine how large the lumped capacitor must be, I made a low-power test using a low-impedance square-wave generator, set to low frequency, in place of the spark gap, and used a variable capacitor as C₂. 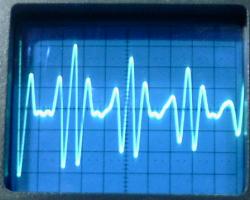The waveforms observed at the transitions of the square wave are similar to the ones that would be observed starting with a charged C₁. The waveforms below were obtained with a lumped C₂ = 62 pF, and the antenna at the top load at its minimum length. They correspond closely to the ideal waveforms.

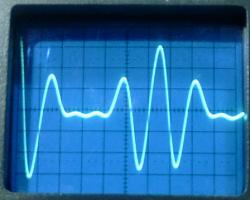
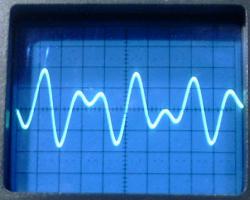
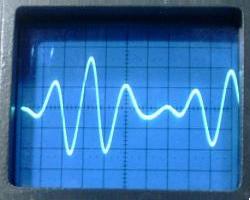
VL₁, VL₂, and VL₃. 2 µs/div.

The energy transfer in 6.6 µs can be observed. The three resonance frequencies were measured as 232, 307, and 385 kHz. The ideal values would be 228, 304, and 380 kHz. The obtained precision was quite good, with errors of 1.8%, -1%, and -1.3% in the frequencies.

Without a lumped C₂, the system falls close to a higher mode, that uses the remaining distributed C₂ = 17.64 pF. The mode 6:7:14 would result in L₁= 61.77 µH, C₂= 24.63 pF, L₂= 3.819 mH, and k₁₂= 0.3453, for the same other elements. The energy transfer for this mode occurs in 3.5 cycles, close to the observed. The input and output voltages are similar to what occurs in a two coils system operating in mode 6:7, a mode that I could obtain with my Tesla coil only when I connected it as an Oudin coil. The magnifier configuration results in faster energy transfer even when a lumped C₂ is not used.

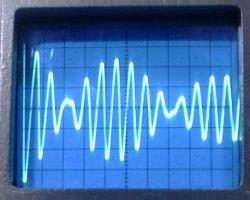
VL₁ with a lumped C₂ and without. 5 µs/div.

The construction of a suitable C₂ is not easy. Simulations show that C₂ has to sustain 26 kV for a gap voltage of 5 kV, during the energy transfer, and somewhat more after the gap quenching. What I tried initially was to make a pair of Leyden jars using plastic cups (polypropylene), each with 124 pF. My reasoning was that with less voltage and more metal area in the capacitors, the losses would be smaller. The performance of the system in a full power test, however, was not as good as the performance of a conventional Tesla coil with the same elements. It was just a bit better than what I had obtained with the directly coupled 6th-order system. Without the lumped C₂, the performance was significantly better, close to the performance of my Tesla coil. C₂ was evidently consuming significant energy, with intense corona around the edges of the plates, and becoming warm quickly. A better approach would be to make a big "mmc" capacitor, by connecting several medium-voltage commercial capacitors in series (look here for a 2:3:4 magnifier made by Terry Fritz).

Another problem that could be causing the poor performance is that with narrow "notches" in the primary waveforms, the primary gap could not be "quenching" (ceasing to conduct) when the energy transfer is complete, while this continued to happen in the version with a distributed C₂ only, that has more gradual "notches". Further tests will reveal what is happening.

Still another possible cause of poor performance is that the rms voltage at the output of a 6th-order system, for the same peak output voltage, is smaller than the rms voltage in a 4th-order system. During the energy transfer, this is caused by the "second order" notches that the 6th-order system produces. Ignoring losses, in a 4th-order system, for all modes the ratio between the rms value of the output voltage and the peak voltage is 0.5 while the gap conducts. For a 6th-order system it varies from 0.4375 for mode 1:2:3 to 0.4330 for high modes (0.4341 for mode 3:4:5). After the quenching of the gap, the oscillation of the energy in the 4th-order system formed by L₂, C₂, L₃, and C₃ may also reduce the rms output voltage.

Spark pictures soon.

Programs that can design and simulate the behavior of this system, and others, can be found here. Extensive materials about Tesla coils can be found in the archives of the Tesla list.

[1] See the papers about "multiple resonance networks" here.

Warning:

This device is powered by a power source that has enough voltage, and specially enough current, to give a fatal shock. The NST, the terminals of C₁, L₁, C₂, L₂, and the spark gap must not be touched in any circunstance while the system is energized. The high-voltage arcs are also not safe to touch. They may cause burns, and the current is intense enough to cause internal body damage.

Created: 11 May 2003 (optimized for 800x600).
Last update: 12 May 2003
Created and maintained by Antonio Carlos M. de Queiroz
See also: Electrostatic Machines